I thought I'd try and give some kind of idea what it is I do every day, without sending everyone to sleep. One of the projects I'm doing right now (hopefully) gives a nice little example!
I'm trying to model how lizards might move through the landscape, in a collaboration with someone who actually knows something about lizards - because there's no point doing modelling if what you're modelling is completely unrealistic!
One current idea I'm working on is the concept that the landscape contains a set number of basking rocks (in this case: 2000, randomly placed in a square kilometre), which every lizard has to have access to in order to survive. So to over-simplify, let's assume that each established lizard has a territory containing one of these basking rocks. Juvenile lizards disperse from their maternal den in order to find their own territory, and we assume that they sprint off in a random direction (they're not very bright), and don't stop until they either find an unoccupied rock or die without a territory. We arbitrarily set the distance they can travel before keeling over to 20 metres. Using this information, we can then generate a map of which rocks are accessible (i.e. within 20 metres) from other rocks, and connect them with lines:
One current idea I'm working on is the concept that the landscape contains a set number of basking rocks (in this case: 2000, randomly placed in a square kilometre), which every lizard has to have access to in order to survive. So to over-simplify, let's assume that each established lizard has a territory containing one of these basking rocks. Juvenile lizards disperse from their maternal den in order to find their own territory, and we assume that they sprint off in a random direction (they're not very bright), and don't stop until they either find an unoccupied rock or die without a territory. We arbitrarily set the distance they can travel before keeling over to 20 metres. Using this information, we can then generate a map of which rocks are accessible (i.e. within 20 metres) from other rocks, and connect them with lines:
One thing that immediately becomes clear is that there are quite a few rocks that are more than 20 metres away from any other rock - this means that any baby lizard trying to find another territory from there will inevitably die, unless their mother has died (giving up her claim to the maternal territory) and it is the first of its siblings to claim it. Clearly, setting a hard limit for the distance a juvenile can travel has serious implications for survival!
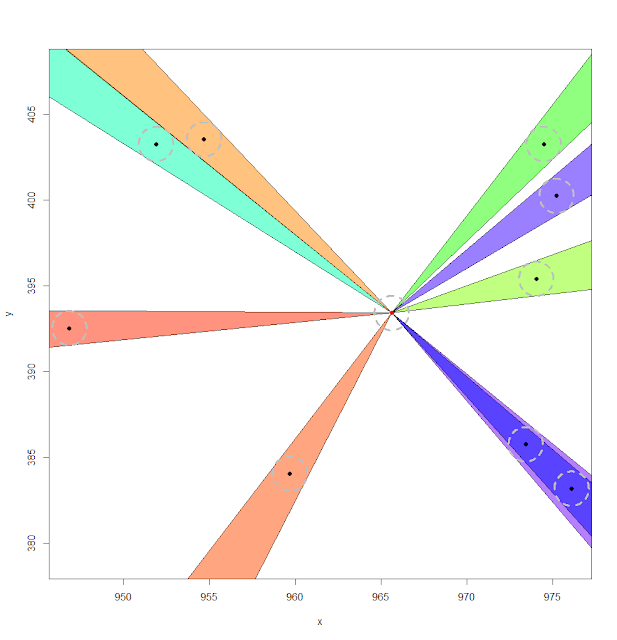
The next problem is to work out how likely a juvenile from a given site is to find another rock (assuming there even are any within 20 metres). As they're not very bright, we assume they'll only stumble across a rock if they travel within one metre of it during their dash to freedom - so we can draw lines that show the range of angles they can travel to find each rock, like below. Though most of them are straightforward to get to, in this example, you can see there is a rock directly behind another rock - so the juvenile will always just choose the first one it reaches. There is also a lot of space between rocks, so a juvenile has to be pretty lucky to be able to establish a territory in the first place!
Things aren't always so straightforward, however. Sometimes a lizard might be lucky and pass one rock just to find another - in the example below, in a couple of places one rock is partially covering the one behind it, but there is a small chance that a lizard will go straight past it and find the rock behind it.
Next time on the mathsy part of the blog, I'm thinking of looking at Snakes and Ladders - and how it gets more complicated when you have to choose between moving multiple tokens - or I could go back to looking at Cribbage like I did a while ago in this post. Any thoughts?


Interesting, however these look like R figures, and hence I believe there is a general lack of c++ in this post. Also, is figure 1 a torus or a sphere? :P
ReplyDelete