Pass the Pigs (Part 1)

So it was only a matter of time before maths started appearing in my blog.  But never fear! This shouldn't be too complicated.  If you do get too freaked out, don't worry, you'll be safer in this part of the blog!

A few weeks ago, my better half and I were having dinner with some dear friends, who proceeded to bring out a game called Pass the Pigs (made by Milton Bradley).  Neither of us had ever seen the game before, but we were quickly introduced and proceeded to have a great time playing it.

The idea of the game is that you roll a pair of pigs, and the position the pigs land in determines how many points you get.  You can stop at any time and "pass the pigs" to the next person.  You can also keep rolling and racking up points, but the downside is that if the pigs land in a certain position, you lose all the points you gained that turn.  If the pigs are touching, you lose all the points you have altogether!

The way to win this game is all about knowing when to quit.  As I was playing, I started wondering if people had worked out optimal strategies for winning this game (because I'm a geek).  The answer as I found out later, is of course yes, yes, yes, and yes.

If you can't be bothered reading all of that, the general idea is that stopping when you've scored 23 points (or, obviously, when you've won the game) is a good strategy.  The actual very best strategy, if you're only playing against one other person, depends on what your score and their score is.  This makes sense if you think about it - if you've only got 10 points and your opponent has 99 points (the score needed to win is 100), there's no point stopping after 22 points because you know your opponent is very likely to win next turn unless you go all-out.

I decided to try and replicate the results.  First I compared the experimental results in all the literature I could find - what chance each "roll" has of happening.  Fortunately, they all seemed to agree pretty well - the consistency is pretty surprising considering we're talking about mass-produced plastic pigs.

Position	Percentage
Side (no dot)	34.9%
Side (dot)	30.2%
Razorback	22.4%
Trotter	8.8%
Snouter	3.0%
Leaning Jowler	0.61%

from Kern, JC (2006). "Pig Data and Bayesian Inference on Multinomial Probabilities". Journal of Statistics Education 14 (3).


So then, using these probabilities, I simulated what would happen if people with different strategies played against each other.  I ran a round-robin competition in which every strategy from "stop at 15" up to "stop at 30" played against each other in a one-on-one game 40,000 times, taking turns to be first to play.


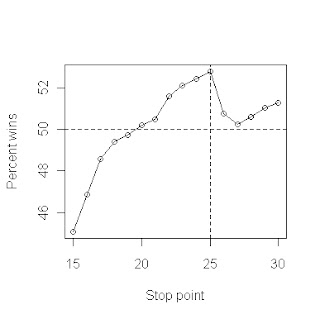
I found that for the first person to play, being more bold is an advantage - the "stop at 25" strategy wins most often, winning over 52% of their games when playing first (see below).  Not bad, considering that all of the strategies are pretty reasonable competitors.  The reason that boldness works here is because the first player gets an advantage in that they will always have played either as many or one more turn than their opponent.  This means that they can get away with taking more risks.

For the second person to play, alternatively being more shy is better - the "stop at 17" and "stop at 18" strategies do best here, again winning over 52% of their games.  The "stop at 17" strategy actually does slightly better, but to such a small extent (52.225% vs 52.219%) that it makes no difference.

If we combine both sets of results, we see that playing to 23 is the best of the strategies, which agrees with what others have said.

Of course, the next question is what to do when playing against more than one opponent?  This is something that strangely hasn't been brought up by anyone, and is a problem for next time.